Concept 14: Parabolas, what are they good for?

Orientation: A satellite receiver is curved so that any signal coming in parallel to its axis of symmetry (any signal coming from very far away, like from a satellite), will reflect off the dish and into the receiver (that pod sticking out in the center).

Vocabulary: The bottom of the dish is called the vertex (V), the point where all the signals converge is called the focal point (F), the line thru V and F is called the axis of symmetry (A of S).

Job 1: Build a satellite dish 5 m across with a focal point of 1.5m from the vertex. What kind of curve satisfies these requirements and how do we find it?

Answer: A parabola satisfies these demands; to learn how to find it, read on.

We need more tools to tackle this project.

Definition: A Parabola is the set of all points in the plane equidistant from a fixed point (Focus) and a fixed line (Directrix (D)). (Derive formula of parabola with F = (0,c) and D y = -c.

Define Length of Latus Rectum (LLR), then have'em graph, and find F, D, V and LLR for:

x² = 8y x² = 12y x² = -16y x² - 3y = 0 x² + y = 0

How about y² = 12x, y² - 6x = 0 ?

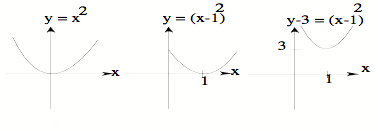
Translation:

General Form:

(y-k)² = 4c(x-h) or (x-h)² = 4c(y-k), Graph, then find F, D, V, & LLR for:

x² + 6x - 8y + 17 = 0 x² + 2x - y = 0 y² + 4y + x + 7 = 0
Reverse ! Now, given the parts, find the equation: Find the equation of the parabola with:

Examples:

Vertex (0,0) and Focus (2,0)

Vertex (-1,2) and Focus (-1,-2)

Focus (-1,-1) and directrix x = 3

Vertex (0,0), A of S is x axis and contains (-3,2)

Vertex (0,0) and contains (-3,-5) and (-3,5)

now finish Job 1, find equation of parabola with Vertex (0,0) and Focus (1.5m), graph it to some scale, scale it up and you're done! If I planned to build it into the ground, how deep must I dig the hole?